Исследование эффективности нечеткого МГУА с различными видами частных описаний и алгоритмами адаптации в задачах прогнозирования 1 часть
УДК 683.519
Авторы: Ю.П. Зайченко, И.О. Заец
Исследование эффективности нечеткого МГУА с различными видами частных описаний и алгоритмами адаптации в задачах прогнозирования
Введение
Данная статья посвящена исследованию и анализу эффективности одного из алгоритмов метода индуктивного моделирования, известного под названием метода группового учета аргументов (МГУА), а именно нечеткого МГУА, в задачах моделирования и прогнозирования макроэкономических процессов. Достоинством МГУА является возможность построения объективной модели в процессе работы алгоритма, а также возможность работать на коротких выборках. Особенностью нечеткого МГУА является получение интервальных оценок для прогнозируемой переменной, что позволяет судить о точности получаемого прогноза.
В работе дается обзор основных результатов, полученных в области нечеткого метода самоорганизации, анализ применения различных видов функций принадлежности (ФП) и алгоритмов пошаговой адаптации, оцениваются перспективы использования нечеткого МГУА в задачах прогнозирования в макроэкономике.
1. Нечеткий МГУА. Построение математической модели
В работах [1-4] была рассмотрена линейная интервальная модель регрессии,
где – нечеткие числа треугольного вида, описываемые парой параметров, где – центр интервала, его ширина.
Тогда – нечеткое число, параметры которого определяются следующим образом.
Центр интервала:
Для того, чтобы интервальная модель была корректной, необходимо, чтобы действительное значение выходной величины принадлежало интервалу неопределенности, что описывается следующими ограничениями:
Предположим, что мы наблюдаем обучающую выборку. Тогда для адекватной модели вида (1) необходимо найти также, для которых бы выполнялись соотношения вида:
Сформулируем основные требования к оценочной линейной интервальной модели для частного описания вида: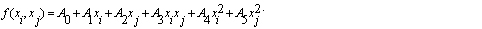
Найти такие значения параметров нечетких коэффициентов, при которых:
а) наблюдаемые значения попадали бы в оценочный интервал для;
б) суммарная ширина оценочного интервала была бы минимальна.
Эти требования можно свести к следующей задаче ЛП [1-3]:

где – номер точки измерения.
Как видим, задача (7) – (9) является задачей ЛП. Однако неудобство формы (7) – (9) для применения стандартных методов ЛП состоит в том, что нет ограничений неотрицательности для переменных. Поэтому для ее решения переходим к двойственной задаче, введя двойственные переменные. Решив двойственную задачу симплекс-методом и найдя оптимальные значения двойственных переменных, определим оптимальные значения искомых переменных,,, а также искомую нечеткую модель для частного описания (6).
В первых работах, посвященных нечеткому МГУА [1,2], рассматривались функции принадлежности нечетких коэффициентов треугольного вида. Поскольку нечеткие числа могут иметь и другой вид ФП, то представляет интерес рассмотрение других классов ФП в задачах моделирования на основе МГУА. В работе [6] рассмотрены нечеткие модели с гауссовскими и колоколообразными ФП.
Назовем нечетким числом с гауссовской ФП нечеткое множество с ФП вида:

Такое НЧ задается парой чисел, где — центр, а — величина, характеризующая ширину интервала (рис.1).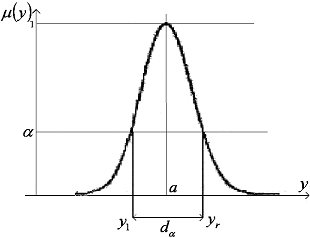
Рис.1. Подмножество уровня a
Пусть оценочная линейная интервальная модель для частного описания НМГУА имеет вид (5). Тогда задача ставится так: найти такие нечеткие числа, т.е. параметры, чтобы:
1) наблюдение принадлежало данному оценочному множеству со степенью, не меньшей, чем,;
2) ширина оценочного интервала уровня была бы минимальна.
Задача нахождения нечеткой модели с гауссовскими ФП сводится окончательно к задаче ЛП следующего вида [6]: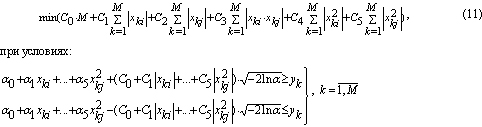
Для решения этой задачи, как и в случае ФП треугольного вида, можно перейти к двойственной задаче ЛП вида:
2. Нечеткий МГУА с различными видами частных описаний
Как известно из общей теории МГУА, модели-претенденты генерируются на основе так называемых частных описаний – моделей определенного вида (например, линейных полиномов), которые, используя в качестве аргументов частные описания предыдущих этапов синтеза модели оптимальной сложности, создают модели-претенденты все более сложной структуры. Но задача выбора вида частных описаний не формализована и возлагается на исследователя. В работах [3-5] в качестве частных описаний предложено использовать ортогональные полиномы Чебышева, Лагерра и тригонометрические полиномы Фурье. Этот выбор обусловлен следующими преимуществами ортогональных полиномов в задачах моделирования нелинейных процессов, характеристики которых априори неизвестны:
• благодаря свойствам ортогональности вычисление коэффициентов полиномиального уравнения, которое аппроксимирует процесс, происходит быстрее, чем для неортогональных полиномов;
• коэффициенты полиномиального аппроксимирующего уравнения не зависят от порядка исходной полиномиальной модели; таким образом, при отсутствии априорной информации о порядке полинома можно проверить несколько порядков, при этом коэффициенты, полученные для низшего порядка, остаются действительными и для высшего. Это свойство наиболее важно при исследовании порядка аппроксимирующего полинома;
• одним из свойств ортогональных полиномов, которые используются в данной работе и являются наиболее широко используемыми в задачах нелинейной аппроксимации, есть свойство почти равных ошибок. Это свойство состоит в том, что ошибка аппроксимации колеблется в середине диапазона измерений между двумя почти одинаковыми границами. Благодаря этому свойству не могут возникать очень большие ошибки, например, выбросы за пределы диапазона данных, для которых проводится аппроксимация; наоборот, в большинстве случаев ошибки малы. Таким образом, происходит «демпфирование» ошибок аппроксимации.
В работе [3] проведены исследования алгоритмов НМГУА с частными описаниями в виде ортогональных полиномов. В результате проведенных экспериментов по прогнозированию макроэкономических показателей Украины- индекса потребительских цен (ИПЦ) и внутреннего валового продукта (ВВП) был сделан вывод о том что наиболее адекватным видом частичных описаний для данного класса задач являются тригонометрические полиномы Фурье, далее следуют полиномиальные в виде квадратичных полиномов и, наконец, наихудшими являются полиномы Чебышева.
Авторы: Ю.П. Зайченко, И.О. Заец
Исследование эффективности нечеткого МГУА с различными видами частных описаний и алгоритмами адаптации в задачах прогнозирования
Введение
Данная статья посвящена исследованию и анализу эффективности одного из алгоритмов метода индуктивного моделирования, известного под названием метода группового учета аргументов (МГУА), а именно нечеткого МГУА, в задачах моделирования и прогнозирования макроэкономических процессов. Достоинством МГУА является возможность построения объективной модели в процессе работы алгоритма, а также возможность работать на коротких выборках. Особенностью нечеткого МГУА является получение интервальных оценок для прогнозируемой переменной, что позволяет судить о точности получаемого прогноза.
В работе дается обзор основных результатов, полученных в области нечеткого метода самоорганизации, анализ применения различных видов функций принадлежности (ФП) и алгоритмов пошаговой адаптации, оцениваются перспективы использования нечеткого МГУА в задачах прогнозирования в макроэкономике.
1. Нечеткий МГУА. Построение математической модели
В работах [1-4] была рассмотрена линейная интервальная модель регрессии,
где – нечеткие числа треугольного вида, описываемые парой параметров, где – центр интервала, его ширина.
Тогда – нечеткое число, параметры которого определяются следующим образом.
Центр интервала:

Для того, чтобы интервальная модель была корректной, необходимо, чтобы действительное значение выходной величины принадлежало интервалу неопределенности, что описывается следующими ограничениями:

Предположим, что мы наблюдаем обучающую выборку. Тогда для адекватной модели вида (1) необходимо найти также, для которых бы выполнялись соотношения вида:

Сформулируем основные требования к оценочной линейной интервальной модели для частного описания вида:
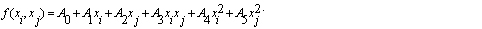
Найти такие значения параметров нечетких коэффициентов, при которых:
а) наблюдаемые значения попадали бы в оценочный интервал для;
б) суммарная ширина оценочного интервала была бы минимальна.
Эти требования можно свести к следующей задаче ЛП [1-3]:

где – номер точки измерения.
Как видим, задача (7) – (9) является задачей ЛП. Однако неудобство формы (7) – (9) для применения стандартных методов ЛП состоит в том, что нет ограничений неотрицательности для переменных. Поэтому для ее решения переходим к двойственной задаче, введя двойственные переменные. Решив двойственную задачу симплекс-методом и найдя оптимальные значения двойственных переменных, определим оптимальные значения искомых переменных,,, а также искомую нечеткую модель для частного описания (6).
В первых работах, посвященных нечеткому МГУА [1,2], рассматривались функции принадлежности нечетких коэффициентов треугольного вида. Поскольку нечеткие числа могут иметь и другой вид ФП, то представляет интерес рассмотрение других классов ФП в задачах моделирования на основе МГУА. В работе [6] рассмотрены нечеткие модели с гауссовскими и колоколообразными ФП.
Назовем нечетким числом с гауссовской ФП нечеткое множество с ФП вида:

Такое НЧ задается парой чисел, где — центр, а — величина, характеризующая ширину интервала (рис.1).

Рис.1. Подмножество уровня a
Пусть оценочная линейная интервальная модель для частного описания НМГУА имеет вид (5). Тогда задача ставится так: найти такие нечеткие числа, т.е. параметры, чтобы:
1) наблюдение принадлежало данному оценочному множеству со степенью, не меньшей, чем,;
2) ширина оценочного интервала уровня была бы минимальна.
Задача нахождения нечеткой модели с гауссовскими ФП сводится окончательно к задаче ЛП следующего вида [6]:
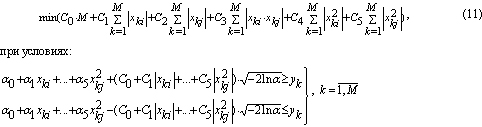
Для решения этой задачи, как и в случае ФП треугольного вида, можно перейти к двойственной задаче ЛП вида:

2. Нечеткий МГУА с различными видами частных описаний
Как известно из общей теории МГУА, модели-претенденты генерируются на основе так называемых частных описаний – моделей определенного вида (например, линейных полиномов), которые, используя в качестве аргументов частные описания предыдущих этапов синтеза модели оптимальной сложности, создают модели-претенденты все более сложной структуры. Но задача выбора вида частных описаний не формализована и возлагается на исследователя. В работах [3-5] в качестве частных описаний предложено использовать ортогональные полиномы Чебышева, Лагерра и тригонометрические полиномы Фурье. Этот выбор обусловлен следующими преимуществами ортогональных полиномов в задачах моделирования нелинейных процессов, характеристики которых априори неизвестны:
• благодаря свойствам ортогональности вычисление коэффициентов полиномиального уравнения, которое аппроксимирует процесс, происходит быстрее, чем для неортогональных полиномов;
• коэффициенты полиномиального аппроксимирующего уравнения не зависят от порядка исходной полиномиальной модели; таким образом, при отсутствии априорной информации о порядке полинома можно проверить несколько порядков, при этом коэффициенты, полученные для низшего порядка, остаются действительными и для высшего. Это свойство наиболее важно при исследовании порядка аппроксимирующего полинома;
• одним из свойств ортогональных полиномов, которые используются в данной работе и являются наиболее широко используемыми в задачах нелинейной аппроксимации, есть свойство почти равных ошибок. Это свойство состоит в том, что ошибка аппроксимации колеблется в середине диапазона измерений между двумя почти одинаковыми границами. Благодаря этому свойству не могут возникать очень большие ошибки, например, выбросы за пределы диапазона данных, для которых проводится аппроксимация; наоборот, в большинстве случаев ошибки малы. Таким образом, происходит «демпфирование» ошибок аппроксимации.
В работе [3] проведены исследования алгоритмов НМГУА с частными описаниями в виде ортогональных полиномов. В результате проведенных экспериментов по прогнозированию макроэкономических показателей Украины- индекса потребительских цен (ИПЦ) и внутреннего валового продукта (ВВП) был сделан вывод о том что наиболее адекватным видом частичных описаний для данного класса задач являются тригонометрические полиномы Фурье, далее следуют полиномиальные в виде квадратичных полиномов и, наконец, наихудшими являются полиномы Чебышева.
Комментарии (0)
RSS свернуть / развернутьТолько зарегистрированные и авторизованные пользователи могут оставлять комментарии.